算法模板--回溯

1.回溯（属于遍历问题，关注树枝）

时间复杂度: O(n!)

抽象地说，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。

站在回溯树的一个节点上，只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

// 只找一个答案：boolean find; if (find) return;
// 找方案数：int res = 0; if (找到)｛res++; return;｝
void backtrack(路径, 选择列表)
    if 满足结束条件｛
        result.add(路径)
        return
    ｝
    for 选择 in 选择列表{
        做选择
        backtrack(路径, 选择列表)
        撤销选择
    }

2.排列/组合/子集问题

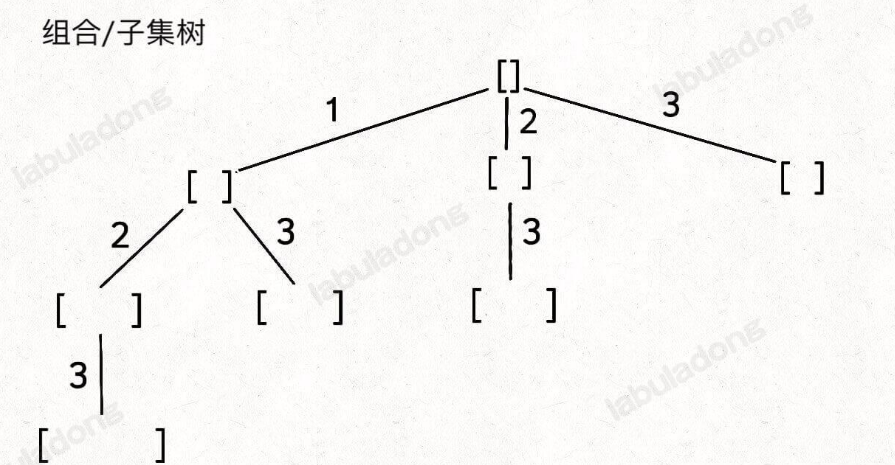
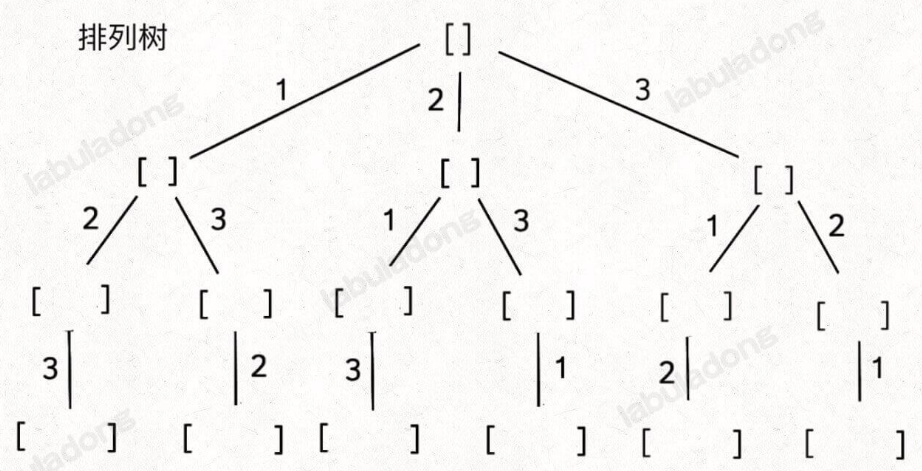
1. 元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，backtrack 核心代码如下：

// 组合/子集问题回溯算法框架
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}

// 排列问题回溯算法框架
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

2. 元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次，其关键在于排序和剪枝，backtrack 核心代码如下：

Arrays.sort(nums);
// 组合/子集问题回溯算法框架
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 剪枝逻辑，跳过值相同的相邻树枝
        if (i > start && nums[i] == nums[i - 1]) {
            continue;
        }
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i + 1);
        // 撤销选择
        track.removeLast();
    }
}


Arrays.sort(nums);
// 排列问题回溯算法框架
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 剪枝逻辑
        if (used[i]) {
            continue;
        }
        // 剪枝逻辑，固定相同的元素在排列中的相对位置
        if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
            continue;
        }
        // 做选择
        used[i] = true;
        track.addLast(nums[i]);

        backtrack(nums);
        // 撤销选择
        track.removeLast();
        used[i] = false;
    }
}

3. 元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次，只要删掉去重逻辑即可，backtrack 核心代码如下：

// 组合/子集问题回溯算法框架
void backtrack(int[] nums, int start) {
    // 回溯算法标准框架
    for (int i = start; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        // 注意参数
        backtrack(nums, i);
        // 撤销选择
        track.removeLast();
    }
}


// 排列问题回溯算法框架
void backtrack(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        // 做选择
        track.addLast(nums[i]);
        backtrack(nums);
        // 撤销选择
        track.removeLast();
    }
}

3.DFS（属于遍历问题，关注单个节点）

void backtrack(...) {
    if (到达叶子节点) {
        return;
    }

    做选择
    ...
    for (int i = 0, i < n; i++) {
        backtrack(...)
    }
    撤销选择
    ...
}

4.DFS和回溯

// 回溯
void backtrack(Node root) {
    if (root == null) {
        return;
    }

    for (Node child : root.children) {
        做选择
        printf("我在 %s 和 %s 中间的树枝上做选择", root, child);

        backtrack(child);

        撤销选择
        printf("我在 %s 和 %s 中间的树枝上撤销选择", root, child);
    }
}

// DFS
void dfs(Node root) {
    if (root == null) {
        return;
    }

    做选择

    printf("我在 %s 节点上做选择", root);

    for (Node child : root.children) {
        dfs(child);
    }

    撤销选择
    printf("我在 %s 节点上撤销选择", root);
}